Spanning tree
In mathematics, a spanning tree is a subgraph of an undirected graph that includes all of the undirected graph's vertices. It is a fundamental tool used to solve difficult problems in mathematics such as the four-color map problem and the travelling salesman problem. Usually, a spanning tree formed by branching out from one of the inner points, which is why it is described as a tree.
Detailed explanation
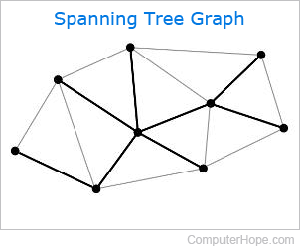
To visualize a spanning tree, first picture an undirected graph: for instance, a random collection of points connected by lines. The connections must be undirected; meaning that you can travel in either direction on the lines to get from one point to another. Every point must connect to the rest somehow, and each point may have multiple connections.
A spanning tree for this graph is any subgraph (a graph using the same points) that touches all the points, but doesn't need to share the same lines.
